 线性回归
线性回归
# 分类问题(classification)
逻辑回归(Logistic Regression)
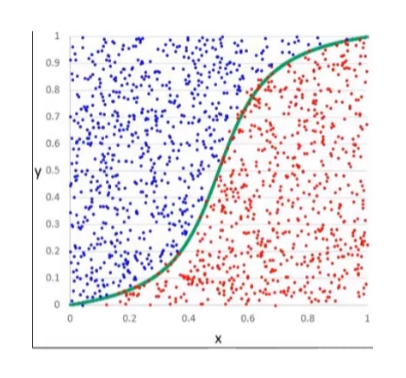
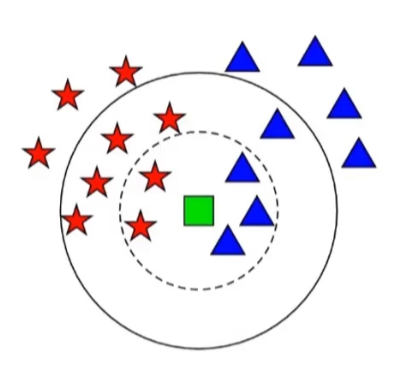
KNN 近邻模型
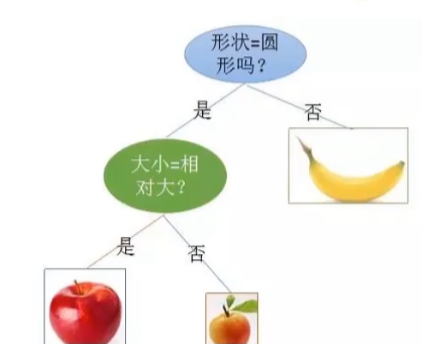
决策树
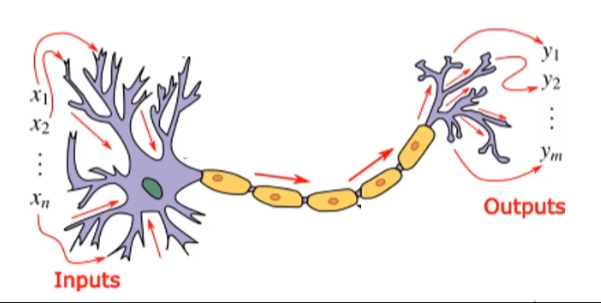
神经网络
分类和回归的区别:
分类:判断类别,非连续型标签(true/false;0/1/2)
回归:建立函数关系,连续型数值(比如 0-200000 的任意数值)
# 逻辑回归
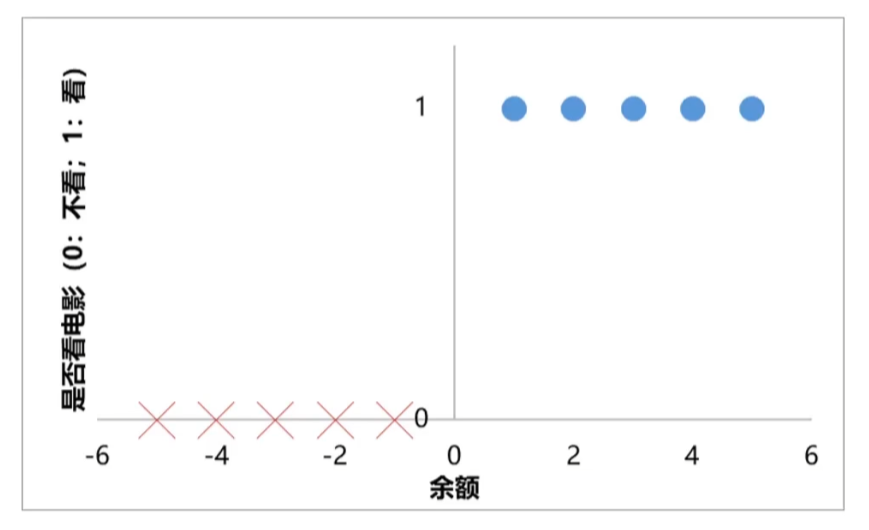
根据余额,判断小明是否会去看电影
训练数据
余额为1、2、3、4、5:看电影(正样本)
余额为-1、-2、-3、-4、-5:不看电影(负样本)
1
2
3
2
3
分类任务基本框架:
1. y = f(x1,x2 … xn)
2. 判断为类别N,如果y=n
1
2
3
2
3
小明是否去看电影:y = f (x) ∈ {0,1}
y=0: 不看电影 (负样本)
y=1: 看电影 (正样本)
先用线性回归模型预测点的分布情况:
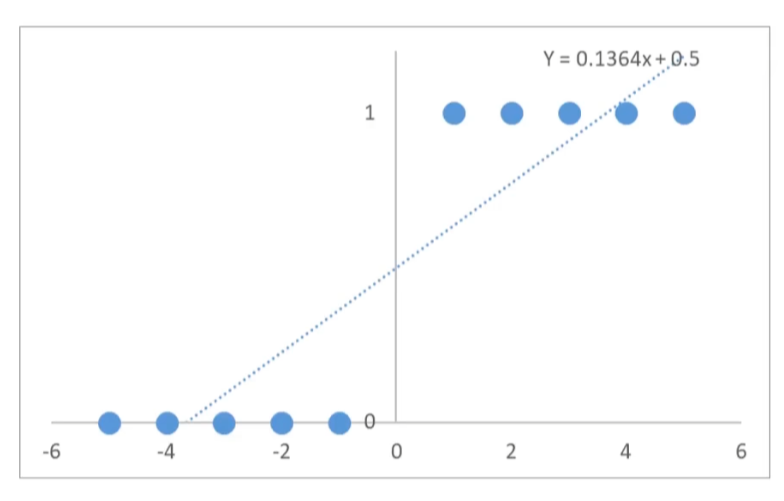
(x1,y1) = (-5,0)
(x2,y2) = (-4,0)
(x3,y3) = (-3,0)
(x4,y4) = (-2,0)
(x5,y5) = (-1,0)
(x6,y6) = (1,1)
(x7,y7) = (2,1)
(x8,y8) = (3,1)
(x9,y9) = (4,1)
(x10,y10) = (5,1)
建立线性回归模型:
y=ax+b
得到适合的 a,b
得到每组 x,y 的预测值
当y>0.5 时,预测为正样本
当y<0.5 时,预测为负样本
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
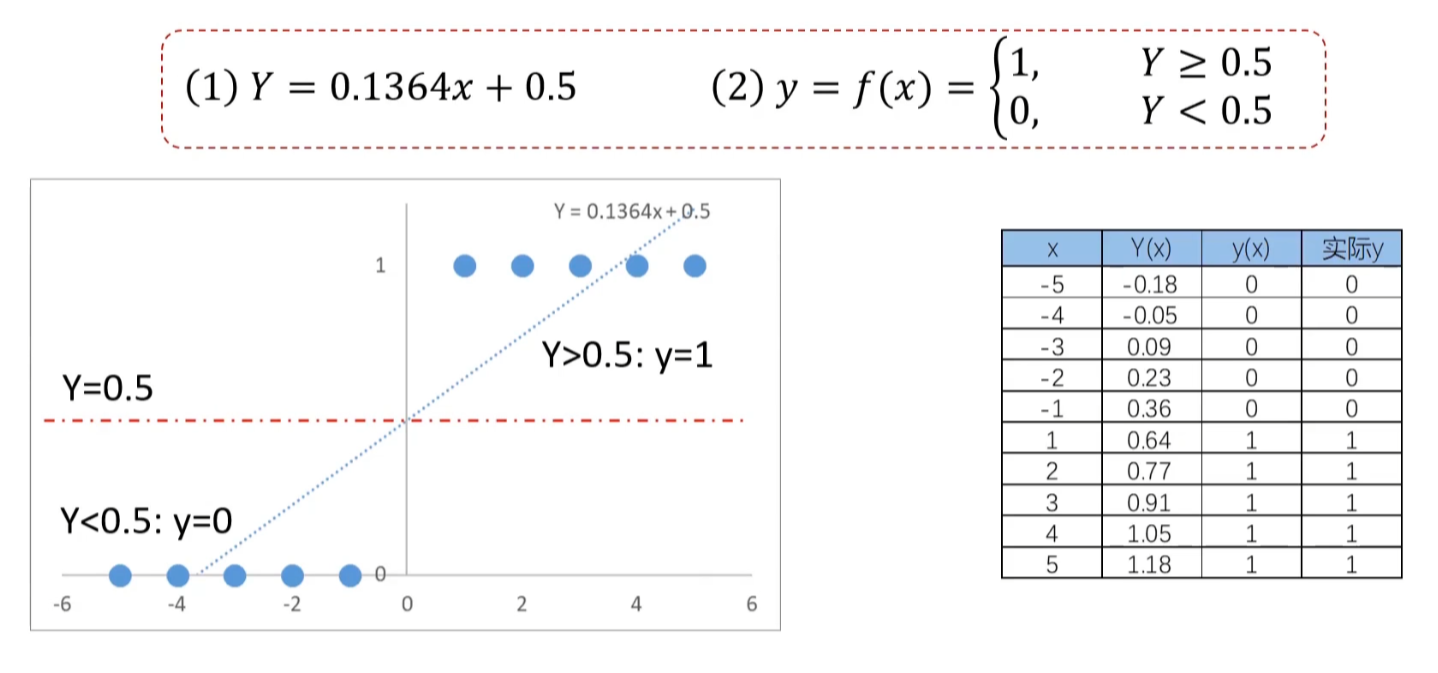
图中计算方式:
0.1364*-5+0.5 = Y(x) = -0.18 < 0.5 = y(x) = 0
1
2
2
这样看起来线性回归效果似乎很不错,但如果样本量变大以后,准确率会下降。
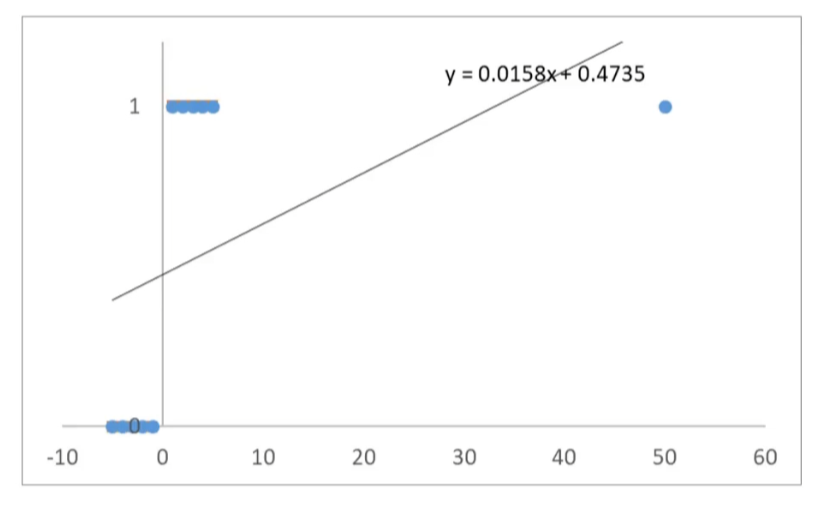
突然小明变得有钱,变为 50,那么 x=50,那么 y 肯定是 = 1 的
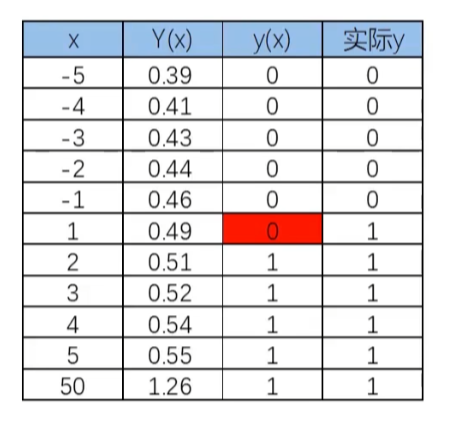
如上图,当 x 距原点边远,预测开始不准确,测试我们可以使用逻辑回归
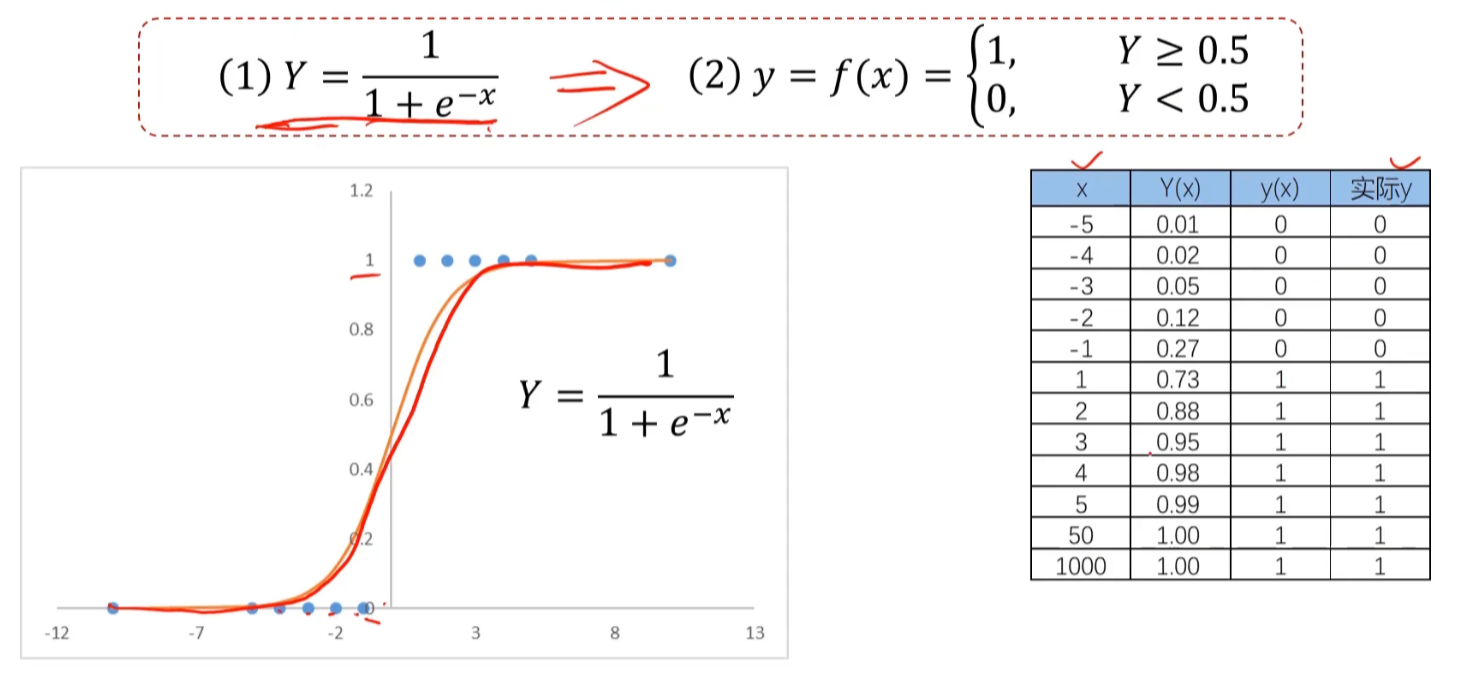
使用逻辑回归你拟合数据,可以很好的完成分类任务。逻辑回归用于解决分类问题的一种模型(Sigmoid 函数)。根据数据特征或属性,计算其归属于某一类别的概率 P,根据概率数值判断其所属类别。主要应用场景:二分类问题。
我们再次计算小明是否会去看电影 (余额为 - 10、100)
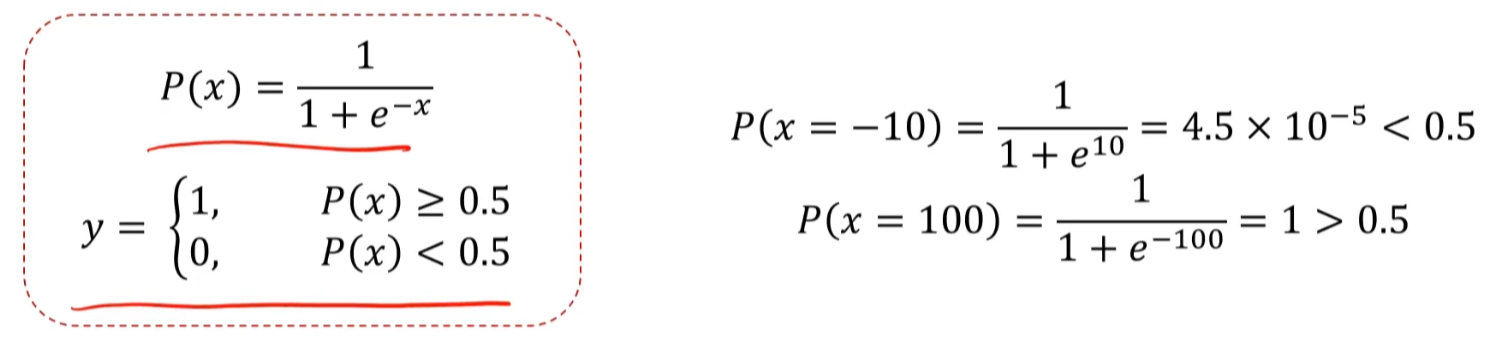
public class SigmoidFunction {
public static void main(String[] args) {
// 测试不同z值的Sigmoid结果
double[] testValues = {-5.0, -2.0, -1.0, 0.0, 1.0, 2.0, 5.0};
System.out.println("z\t\tsigmoid(z)");
for (double z : testValues) {
double result = sigmoid(z);
System.out.printf("%.1f\t\t%.15f%n", z, result);
}
}
/**
* 计算Sigmoid函数 σ(z) = 1 / (1 + e^(-z))
* @param z 输入值
* @return Sigmoid函数结果
*/
public static double sigmoid(double z) {
// 直接使用公式计算
return 1.0 / (1.0 + Math.exp(-z));
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# 复杂逻辑回归
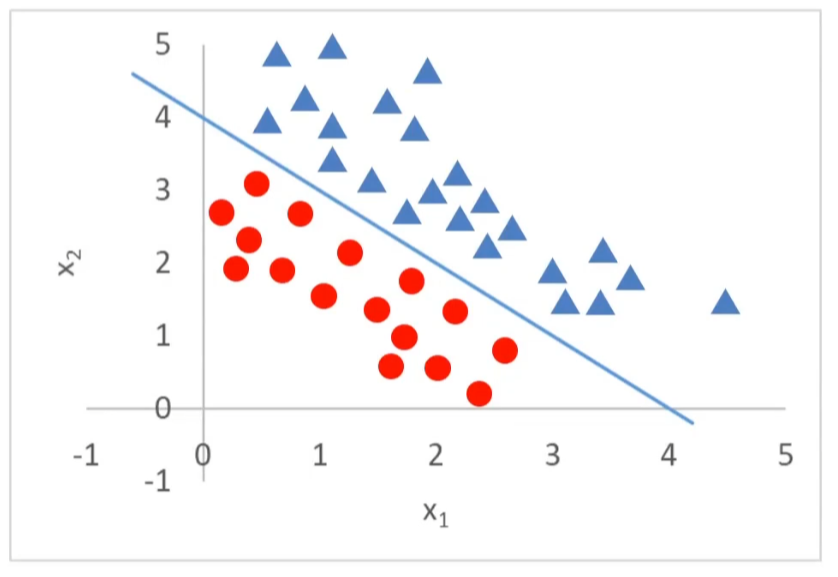
之前小明是否还有钱属于一个维度,上图呢分为 x1 和 x2,有两个维度,所以改变公式
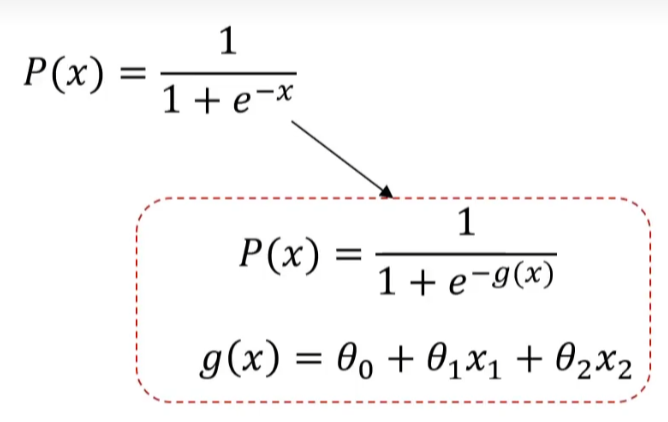
图中就是把一维 -x 变为 -g (x) 多维函数,对于上图核心就是找到 g (x) 的值
上次更新: 1/1/2026, 8:54:37 PM
